Factor analysis of EBI items: Tutorial with RStudio and EFA.dimensions package

 For this posting, I will be walking you through an example of exploratory factor analysis (EFA) using RStudio with the EFA.dimensions package. In this tutorial, I will address various steps one typically considers when performing EFA and how to make decisions at various stages in the process. 

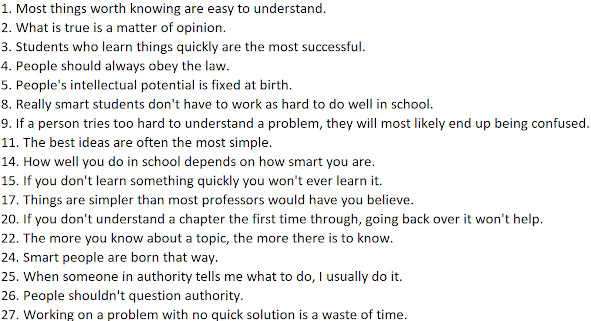
We will be factor analyzing items from the Epistemic Belief Inventory (EBI; Schraw et al., 2002) based on data collected from Chilean high school students in this study. Download a copy of the Excel file containing the data here. The items for our analyses all have the root name 'ce' (see screenshot below). Although the original authors of the study analyzed all 28 items, to keep our output simpler, we will only perform the analysis on the 17 items contained in Table 2. 

These items correspond to the following variables in the Excel data file: ce1, ce2, ce3, ce4, ce5, ce8, ce9, ce11, ce14, ce15, ce17, ce20, ce22, ce24-ce27. Below is a screenshot of a subset of the Excel file.

Video walk-through of the steps described below. 

Preliminaries

For our demonstration, we will rely on two R packages: EFA.dimensions and the psych package. You will need to make sure these are installed and called up (using the 'library' function) so they are active. The commands below show the use of the library function to activate those packages. Additionally, to simplify some of our references to the data during our analysis, I have included code (see line 3) where I am saving columns 1 - 5, 8, 9, 11, 14, 15, 17, 20, 22, 24:27 of the original data frame (after importation) into a new data frame called 'itemdata'. These columns correspond to the EBI items noted previously.  

Here is a text file containing all the commands we will be using below: text file

The analyses

Step 1: Assess factorability of correlation matrix

[For this step, we will assume you have already examined the distributions of your variables and considered factors that may have impacted the quality of the correlations being submitted to factor analysis.]

The first question you need to ask yourself during EFA is whether you have the kind of data that would support factor analytic investigation and yield reliable results. Some issues can produce a factor solution that is not particularly trustworthy or reliable (Cerny & Kaiser, 1977; Dziuban & Shirkey, 1974), whereas others can result in algorithmic problems that may prevent a solution from even being generated (Watkins, 2018). The way to address this question is to evaluate the correlation matrix based on the set of measured variables being submitted to factor analysis. [In the current example, the measured variables are the items from the EBI. Hereafter, I will be referring to "items" throughout the discussion.] Answering the question of whether it is appropriate to conduct factor analysis in the first place can assist you in correcting problems before they emerge during analysis or (at the very least) serve as valuable information that can assist you in diagnosing problems that occur when running your EFA.     

A common preliminary step is to examine the correlation matrix based on your items for the presence of correlations that exceed .30 (in absolute value; Watkins, 2022). During factor analysis, the idea is to extract latent variables (factors) to account for (or explain) the correlational structure among a set of measured variables. If the items in your correlation matrix are generally trivial (i.e., very small) or near zero, this logically precludes investigation of common factors since there is little common variation among the variables that will be shared. Additionally, when screening your correlation matrix, you should also look for very high correlations (e.g., r's > .90) among items that might suggest the presence of linear (or near-linear) dependencies among your variables. The presence of multicollinearity among your variables can produce unstable results, whereas singularity in your correlation matrix will generally result in the termination of the analysis (with a message indicating your matrix is nonpositive definite). In the presence of singularity, certain matrix operations cannot be performed (Watkins, 2021). [Note: A common reason why singularity occurs is when an analyst attempts to factor analyze correlations involving a set of items along with a full scale score that is based on the sum or average of those items. An example of the warning message in R/RStudio can be seen here]   

To examine our correlation matrix, we will rely on the corr.test function associated with the psych package. Line 9 (below) in the Script Editor below contains the corr.test function and associated arguments for our analysis. The 'itemdata' reference is in the data argument portion of the command. This points RStudio to the data frame containing the variables we are analyzing. Setting use="complete.obs" invokes listwise deletion of cases during this analysis that have missing data on any of the variables included in the correlation matrix. To generate the correlation matrix, simply highlight line 9 and click Run.

The matrix is symmetric with 1's on the principal diagonal. If you wish to count the number of unique correlations greater than .30 (in absolute value), simply count the number in either the lower OR upper triangle. Counting the number of correlations in the lower triangle of this matrix, there look to be about 10 correlations [out of the p(p-1)/2 = 17(16)/2 = 176 unique correlations; remember, the matrix is symmetric about the principal diagonal containing 1’s] that exceed .30. None of the correlations exceed .90, which indicates to me low likelihood of any linear dependencies. 

The next set of output further allows us to examine the appropriateness of the correlation matrix for factor analysis. This output was generated using the function, 'FACTORABILITY' (which is associated with the EFA.dimensions package). Line 11 contains the function and arguments to generate the relevant output. Highlight this line and click Run to generate the output. 

Bartlett’s test is used to test whether your correlation matrix differs significantly from an identity matrix [a matrix containing 1’s on the diagonal and 0’s in the off-diagonal elements]. In a correlation matrix, if all off-diagonal elements are zero, this signifies your variables are completely orthogonal. Failure to reject the null when performing this test is an indication that your correlation matrix is factorable. In our output, Bartlett’s test is statistically significant (p<.001). [Keep in mind that Bartlett's test is often significant, even with matrices that have more trivial correlations, as the power of the test is influenced by sample size. Factor analysis is generally performed using large samples.]

The determinant of a correlation matrix can be thought of as a generalized variance. If this value is 0, your matrix is singular (which would preclude matrix inversion). If the determinant is greater than .00001, then you have a matrix that should be factorable. In our results, the determinant is .113, which is greater than .00001.

The KMO MSA is another index to assess whether it makes sense to conduct EFA. Values closer to 1 on the overall MSA indicate greater possibility of the presence of common factors (making it more reasonable to perform EFA). 

Here, we see the overall MSA is .78, which falls into Kaiser and Rice’s (1974) “middling” (but factorable) range [see scale below]. The remaining MSA’s are item-level measures. Values with KMO values < .50 are candidates for removal prior to running your EFA. The item (variable) level MSA’s in our data range from .67 to .85, suggesting it is reasonable to submit them all to EFA.

Step 2: Determination of number of factors

Once you have concluded (from Step 1) that it is appropriate to conduct EFA, the next step is to estimate the number of factors that may account for the interrelationships among your items. Historically, analysts have leaned on the Kaiser criterion (i.e., eigenvalue cutoff rule) to the exclusion of better options. This largely seems to be the result of this criterion being programmed into many statistical packages as a default. Nevertheless, this rule often leads to over-factoring and is strongly discouraged as a sole basis for determining number of factors. 

Ideally, you will try to answer the 'number of factors question' using multiple investigative approaches. This view is endorsed by Fabrigar and Wegener (2012) who stated, “determining the appropriate number of common factors is a decision that is best addressed in a holistic fashion by considering the configuration of evidence presented by several of the better performing procedures” (p. 55). It is important to recognize, however, that different analytic approaches can suggest different possible models (i.e., models that vary in the number of factors) that may be explain your data. Resist the temptation to run from this ambiguity by selecting one and relying solely on it (unless perhaps it is a method that has a strong empirical track record for correctly identifying factors; a good example is parallel analysis). Instead, consider the different factor models[or at least a reasonable subset of them] as 'candidates' for further investigation. From there, perform EFA on each model, rotate the factors, and interpret them. The degree of factor saturation and interpretability of those factors can then be used as a basis for deciding which of the candidate models may best explain your data.  

Method 1: Parallel analysis

Parallel analysis is a method that has strong empirical support as a basis for determining the number of factors. This method involves comparing eigenvalues from your data against eigenvalues that have been generated at random. To perform parallel analysis, use the 'RAWPAR' function associated with the EFA.dimensions package. The factormodel="PCA" argument instructs the function to compute the real and random eigenvalues using an unreduced correlation matrix (essentially extracting eigenvalues using the principal components method) The Ndatasets=1000 argument instructs the function to generate the random eigenvalues using 1000 simulations. The percentile=95 argument instructs the function to return the 95th percentiles for the randomly generated eigenvalues. See line 13 below. 

One you have generated the output using the 'RAWPAR' function, simply compare the eigenvalues from your data [see Real Data column below] against randomly generated eigenvalues [either Mean or 95^th percentile]. Using this method, the number of factors equals the number of Real Data eigenvalues that exceed those that were randomly generated. Looking at the table below, we see that the eigenvalues from our data exceed the 95^th percentile of randomly generated eigenvalues. This suggests retention of 3 factors. 

There is debate within the factor analytic literature as to whether parallel analysis should be performed using the unreduced correlation matrix [see Horn's (1965) parallel analysis] or using a reduced correlation matrix [see Humphrys and Montanelli (1975) approach to parallel analysis]. Without wading into this debate, I provide the code (below) for conducting parallel analysis on the reduced correlation matrix. Notice the only difference is the argument for factormodel, which now reads factormodel="PAF". [The PAF refers to principal axis factoring.] See line 15 below.

As you can see next, using the reduced correlation matrix resulted in the estimated number of factors as four. [Recall, I mentioned that different methods will not all necessarily agree.] Some research has investigated conditions under which parallel analysis on the reduced versus unreduced correlation matrix results in a better estimate for the number of factors. For more information, you might check out Crawford et al. (2010).

Method 2: MAP test

This method involves a comparison of PCA models that vary in number of extracted components. The starting point for the method is to extract 0 components and simply compute the average of the squared zero-order correlations among a set of variables. Next, a single component (i.e., 1 component model) is extracted and the average of the squared partial correlations (i.e., after partialling the first component) is computed. Following, two components are extracted (i.e., 2 component model) and the average of the squared partial correlations (i.e., after partialling the first two components) is computed; and so on. The number of recommended factors based on this procedure is associated with the component model that has the smallest average (partial) correlations. To generate the MAP (i.e., Minimum average partial) Test, use the 'MAP' function with EFA.dimensions. See line 17 below.

In the output below, the ‘root’ column refers to the number of principal components extracted and the ‘Avg. corr. Sq’ column contains values we use to compare different models. Against, the preferred model of all the candidate models has the smallest average (squared) correlation (from column 2). In the current output, the smallest average squared correlation (.01315) is associated with a principal components model where one component has been extracted. This provides an estimate of one possible factor that explains the associations among our indicator variables.  

Method 3: Scree test

The scree test is one of the older methods for identifying number of factors. This test involves plotting the eigenvalues (Y axis) against factor number (X axis). In general, the plot of the eigenvalues look like the side of a mountain with the base of the mountain containing 'rubble'. To obtain the scree plot using EFA.dimensions, use the 'SCREE_PLOT' function. Here, I have typed the function into line 19 in the Script Editor.

Here is the output generated using this function...

To perform the analysis, you simply look for the 'elbow' that demarcates between the major factors [found on the main slope(s)] and the trivial factors [found at the base]. For instance, we can visualize the 'elbow' occurring in the graph after the third factor [technically, the roots here are principal components, but we are using these to estimate number of factors]. This would suggest a three-factor solution may be tenable.

A limitation of the scree plot is its subjectivity. Moreover, there are times when there may be other 'break-points' that can cloud the picture of how many factors to retain. 

Method 4: Sequential chi-square tests

Another option for identifying the possible number of factors is to use sequential chi-square tests. Personally, I am not of a big fan of this approach given that it is well known to lead to over-factoring, and this tendency will be amplified in larger samples. The approach involves testing the fit of a set of common factor models, each containing a different number of factors. The significance test associated with each factor model is a test of whether the model deviates significantly from an exact fitting model. In effect, the significance tests that are performed are essentially a series of 'badness of fit' tests. The preferred factor model (in terms of number of factors) is the one that has the fewest factors and is not statistically significant. To perform this test using EFA.dimensions simply use the 'SMT' function. See line 21.

In the output below, we see 8 factor indicated. Given our very large sample size - and the much smaller number of factors associated with the other procedures - my assumption is this is due to the chi-square tests being overpowered.

Method 5: Empirical Kaiser criterion.

This method was proposed by Braeken and van Assen (2017) as an alternative to the more deeply flawed Kaiser (1960) criterion (i.e., eigenvalue cutoff rule of 1). The basic approach is to compare the eigenvalues from your data (column 2) against a set of reference values that "can be seen as a sample-variant of the original Kaiser criterion (which is only effective at the population level), yet with a built-in empirical correction factor that is a function of the variables-to-sample-size ratio  and  the  prior  observed  eigenvalues  in  the  series" (p. 463). According to Braeken and van Asson (2017), the EKC appears to function as well or better than parallel analysis, with the EKC outperforming parallel analysis in cases where factors are moderately to highly correlated and there are few measured variables per factor. In a manner analogous to what we did before with parallel analysis, we retain those factors that have eigenvalues from the data that exceed the reference values. The EFA.dimensions function for performing this test is 'EMPKC'. See line 23 below.

We see below, that the method suggests maintaining 3 factors. [It turns out that if we’d used the traditional Kaiser criterion of maintaining factors with eigenvalues > 1, it would have also suggested 3 factors.]

***********************************************************************************

Overall, the results of Step 2 suggest the presence of anywhere from 1 to 8 factors. In general, the three factor model garnered the most support. The Sequential chi-square test results do not appear particularly trustworthy, especially given the very large sample size (n=1039). The MAP test result does not seem very likely given our knowledge that beliefs about knowledge and learning (what the EBI is designed to measure) are currently understood to be multidimensional. For our next step, we will force a three-factor solution and interpret both Promax and Varimax rotated solutions.

For a closer look at the table, click here.

***********************************************************************************

Step 3: Final extraction of factors, rotation, and interpretation

At this point, I have determined the most likely candidate is a model containing three factors [The one-factor model suggested by the MAP test is unlikely, especially given evidence epistemic beliefs are multidimensional]. For this reason, the remainder of this discussion will be based on a three-factor model. To perform the analysis, we will rely on Principal Axis Factoring (PAF) for factor extraction. Watkins (2018) notes factor extraction involves transforming correlations to factor space in a manner that is computationally, but not necessarily conceptually, convenient. As such, extracted factors are generally rotated to "achieve a simpler and theoretically more meaningful solution" (p. 231). For our example, we will consider two factor rotation approaches (Promax and Varimax) to facilitate interpretation of the final set of factors that are extracted. Promax rotation is one type of oblique rotation that relaxes the constraint of orthogonality of factors, thereby allowing them to correlate. Varimax rotation is a type of orthogonal rotation. When Varimax rotation is used, the factors are not permitted to correlate following rotation of the factor axes. Below is the Script Editor with the code for performing PAF, forcing 3 factors, and then rotating for interpretation. See lines 25 and 27 below.

PAF with Promax rotation

The syntax below is for performing Principal Axis factoring (PAF) with Promax rotation. The 'itemdata' is listed first to refer to the data frame where are data are located. The argument, corkind="pearson", specifies we are analyzing Pearson correlations. The Nfactors=3 argument specifies we are forcing the extraction of 3 factors (recall, this was based on our assessment of the number of factors during Step 2). The iterpaf=50 argument specifies a maximum number of iterations for estimation of the parameters in the model. [If the model does not converge within this maximum, you can re-set this to a higher number.] The rotate="PROMAX" argument specifies (you guessed it!) Promax rotation. Prior to rotation, the extracted factors are orthogonal and account for additive variation in the set of measured variables (items). Promax rotation is an oblique rotation that allows factors to be intercorrelated - this in contrast to Varimax rotation (an orthogonal rotation) which we use later. Finally, the ppower=3 argument is recommended in the package. The aim with this parameter is to give the simplest structure with the lowest inter-factor correlations.

The output 

 The table below contains initial and extracted communalities. During principal axis factoring (PAF) the values in the first column (Initial) are placed into the principal diagonal of the correlation matrix (instead of 1's). It is this reduced correlation matrix that is factored. The Initial communalities are computed as the squared multiple correlation between each measured variable (item) and the remaining variables (items). [You can easily generate these by performing a series of regressions where you regress each variable onto the remaining variables and obtaining the R-squares.] The Extraction communalities are final estimates of the proportion of variation in each item accounted for jointly by the set of common factors that have been extracted. 

The next table in the output are actually not results from the PAF. Rather they are results from an initial Principal components analysis. Personally, I am not entirely sure why this is presented. The eigenvalues in the first column of values indicate the amount of variation in the set of items accounted for by each component that is extracted. Confusingly, the first column refers to 'factor' number (instead of component the component number). I have to assume this is a holdover from the long tradition in EFA to use principal components as estimates of factors and the tendency to use the term 'factors' instead of 'components'. When discussing this table, I will stick with tradition (with the proviso that these are technically components). 

The eigenvalue associated with a given component summarizes how much variation is accounted for in the original set of variables (items) by a given component. The first component accounts for as much variation as 3.06 of the original measured variables (items). We can compute the % of variance by dividing the eigenvalue by the total number of items (i.e., 17): 3.06/17 = .18 (or 18%). The second component accounts for as much variation as 2.04 of the original items. This translates into 2.04/17 = .12 (or about 12% of the variation). Cumulatively, the first and second components account for 30% of the variation in the items. Component 3 accounts for as much variation as 1.43 items, which is approximately (1.43/17)*100% = 8% of the variation. Cumulatively, Components 1-3 account for approximately 38% of the variation in the items. Notice that the fourth component explains less variation than a single measured variable. And so on. 

*It is worth noting the original Kaiser criterion (eigenvalue cutoff rule) was developed as a basis for determining number of factors based on a PCA solution (such as the one above). The reasoning was that for a factor to be useful, it needs to explain as much variation as at least one measured variable. If we applied the eigenvalue cutoff rule to this table (to determine number of factors), it would suggest retention of 3 factors. [The eigenvalues in this table are the same as those we saw earlier in the output when we used the EKC approach to determining number of factors.]

The output you see next reflects the fact that PAF typically proceeds in an iterative fashion [there is a non-iterated principal factors approach, but that is not what we are working with here]. The statement is simply indicating that 9 iterations were required to arrive at a final PAF solution.

Once our factors have been extracted (using PAF), we are presented with output containing information on the variation accounted for in our items by the factors as well as information concerning the relationships between the factors and our items. The next set of output contains a Pattern matrix with unrotated factor loadings. The loadings are zero-order correlations between the EBI items and the factors that have been extracted. Notice that each indicator has a loading on each factor. 

The table below contains the eigenvalues and proportion of variance in the EBI items accounted for by each of the three unrotated factors. The eigenvalues (contained in the Sums of Squared Loadings column) can easily be computed by summing the squared loadings in each column in the matrix above. For example, the eigenvalue associated with Factor 1 is computed as follows: (.10)²+(.00)²+(.54)²+...+(.53)² = 2.34. The eigenvalue for Factor 2 is computed as (-.33)²+(-.36)²+(-.09)²+...+(.25)² = 1.35. The eigenvalue for Factor 3 is computed approximately as (-.30)²+(-.43)²+(-.03)²+...+(.01)² = .70. The Proportion of Variance for Factor 1 is computed as 2.34/17 = .137 (or roughly 14%). The Proportion of Variance for Factor 2 is computed as approximately 1.35/17 = .079 (or roughly 8%). The Proportion of Variance for Factor 3 is computed as roughly .70/17 = .04 (or 4%). Jointly, the factors account for 26% of the variation in the EBI items. 

Additional note: I mentioned above that the final communalities represent the proportion of variation in the measured variables (items) that are accounted for by the set of extracted factors. These communalities can be computed as the sum of squared loadings in each row of the matrix containing the unrotated loadings. For example, the communality for ce1 is computed as (.10)²+(-.33)²+(-.30)² = .2089. In other words the three common factors jointly accounted for roughly 21% of the variation in ec1. The communality for ec5 is computed as (.52)²+(.06)²+(.03)² = .2749. The three common factors accounted for roughly 28% of the variation in ec5.

 

The loadings in the unrotated factor pattern matrix are generally not interpreted and are not particularly useful in providing conceptual clarity when attempting to make sense of the factors that have been extracted. The next set of output contains matrices that are useful for naming the factors and understanding their relationships. 

The first matrix below is referred to as a rotated factor pattern matrix. The loadings in this matrix are akin to standardized regression coefficients (Watkins, 2018). The loading for a particular item on a given factor represents the association between the item and factor after partialling the other factors from that association.

The next matrix is a Structure matrix. This matrix contains the zero-order correlations between each item and the latent factors. Unlike the pattern matrix above, the loadings do not partial the remaining factors from the association between an item and a given factor. 

 

The Pattern matrix and Structure matrix are used to give verbal meaning (or name) the latent factors. When the factors are rotated, the idea is to create a structure whereby each factor has a mixture of higher and lower (near zero) loading items and each item loads nontrivially on at least one - preferably only one - of the latent factors (Pituch & Stevens, 2016). The analyst examines the pattern of loadings on each factor and then using the items that load non-trivially to name/define that factor. Different analysts have different minimum loading criteria (for an item to be used in naming a factor) they rely on, but in general these will fall somewhere in the |.30| to |.40| range (Watkins, 2018). The idea is to define factors using indicators that are large enough to be of practical use. Keep in mind that positive loadings mean that an item is positively related to the underlying factor; negative loadings mean an item is negatively related to the factor. Following an oblique rotation - such as Promax - the primary matrix you should be analyzing to name the factors is the Pattern matrix.

Below, I provide the rotated factor pattern loadings for each of the items and the three factors. For this example we will use a loading criterion of |.30|. Values meeting this criterion are displayed in bold. The sign of the factor loadings convey information regarding the direction of the relationship between the items and the rotated factors. Within the same factor, positive and negative loadings also indicate items that are related to that factor in opposite directions. 

For a closer look at the table, click here.

On Factor 1, ce3, ce5, ce8, ce9, ce14, ce15, ce20, ce24, and ce27 all met the loading criterion. Thematically, the items on Factor 1 appear to represent an amalgam of beliefs that intellectual ability is fixed at birth and that learning is something which occurs quickly or not at all. We will call this factor 'Belief in Fixed ability and Quick Learning'. All the aforementioned items have positive loadings, indicating they are positively associated with the factor. This also means that if we compute scores for this factor, higher values would represent a greater belief in fixed ability and quick learning, whereas lower scores would represent a lesser belief in fixed ability and quick learning.

On Factor 2, ce4, ce25, and ce26 met the loading criterion. Thematically, they reflect a belief that knowledge stems from omniscient authority. We will name this factor 'Belief in Omniscient Authority'. All the items meeting our loading criterion on this factor have negative loadings, meaning they are negatively related to the factor. The negative loadings does not affect the grouping of the items into the 'omniscient authority' factor according to thematic content. However, it does affect the meaning of the poles for the factor. If I compute scores on this factor for individuals in this study (based on the loadings in the pattern matrix), higher scores would represent less of a belief in omniscient authority and lower scores would represent more of a belief in omniscient authority. 

If the negative signs of these loadings confuse you [based on the expectation the loadings should be positive], you can easily multiply all loadings for this factor by -1 and report on these. Indeed, since participants in the original study responded to the survey items using a 1=strongly disagree to 5=strongly agree scale, one might logically assume a respondent indicating strong agreement (5) to a statement on this factor would have a greater belief in omniscient authorities (and thus would score higher on the latent factor) than a person who strongly disagrees (1) with the statement. To change the direction of the poles for the factor in order to make them congruent with this assumption, you can simply multiply all the loadings by -1 and report on those.  

For Factor 3, ce1, ce2, ce11, ce17, and ce22 all met the loading criterion. The items ce2 and ce22 were (originally) negatively-worded items and were reverse-coded by the researchers prior to inclusion in the factor analysis (so that higher values would reflect more naïve epistemic beliefs - which is consistent with the meaning of higher values on the other items). Thematically, the set of items meeting the loading criterion on Factor 3 appears to reflect the belief that knowledge is simple and certain. We will name this factor 'Belief in simple and certain knowledge.' As with Factor 2 ('omniscient authority'), the factor loadings of the aforementioned variables for Factor 3 ('simple and certain knowledge') are all negative in the output. As such, poles of the factor range are reversed from what one might ordinarily expect (i.e., lower scores on the factor indicate greater belief in simple and certain knowledge and higher scores reflect lower belief in simple and certain knowledge). The same logic where you can report on -1 * ALL the loadings on the factor applies here as well. 

*Although it is not an issue during our current analysis, you should avoid retaining and interpreting factors with fewer than three indicators at or near zero (and failing to meet your loading criterion). Three indicators is an absolute minimum number you should accept with with respect to a factor (Hahs-Vaughn, 2016). Factors defined by fewer than three indicators tend to be unreliable and are less likely to show up in future studies. All factors in the pattern matrix had 5-6 items that met the loading criterion and was able to be used to name the factors.

Next, we see the Rotated Sums of Squared Loadings. These are the eigenvalues for the three rotated factors. [They are computed as the sum of squared loadings from the Structure Matrix. Since the factors, following Promax (oblique) rotation, are correlated, we are no longer able to talk in terms of the variance each contributes independently to the explained variation in the items.   

The final matrix in our output contains the correlations among the Promax rotated factors. Factor 1 exhibited a very small, negative correlation (r=-.16) with Factor 2 and a small negative correlation (r=-.10) with Factor 3. Factor 2 and Factor 3 correlated at r=.34. 

To understand the meaning of these correlations, you need to think about the poles of the factors (described above). If I compute scores for Factor 1 ("Belief in Fixed Ability and Quick Learning") based on the original rotated pattern matrix, lower scores would indicate less of a belief in fixed ability and quick learning and higher scores would represent greater belief in fixed ability and quick learning. If I compute scores for Factor 2 ("Belief in Omniscient Authority"), lower scores on the factor would indicate greater belief in omniscient authority and higher scores would indicate lower belief in fixed ability. If I compute scores for Factor 3 ("Belief in Simple and Certain Knowledge") based off the original pattern matrix, lower scores on the factor would indicate greater belief in simple and certain knowledge and higher scores would indicate lower belief in simple and certain knowledge. As produced here, the correlation between Factor 1 and Factor 2 indicates belief fixed ability and quick learning is actually positively related to belief in omniscient authority (given the reversal of the poles for this factor) and to the belief in simple and certain knowledge (again, given the reversal of the poles for this factor). Since both Factors 2 and 3 contain the same reversal of the poles, the positive correlation (r=.34) is interpreted to mean that greater belief in omniscient authority is associated with greater belief in simple and certain knowledge (and less belief in omniscient authority is associated with less belief in simple and certain knowledge). 

***********************************************************************************

Having a background in using the EBI, I personally found the negative loadings for Factors 2 and 3 confusing when I was re-analyzing this data at first using the EFA.dimensions package. This was made even more confusing by the fact that this issue did not appear when I analyzed the data using other programs. Here is an example of a pattern matrix generated using SPSS. The loadings are very similar in magnitude [so ignore the small differences]. But notice the difference in Factors 2 and 3 in terms of the signs of the factor loadings. They appear reversed. 

The reversals in the signs of the loadings also contributes to the differences we observe in the factor correlation matrix between SPSS and the EFA.dimensions package. [Again, ignore the minor discrepancies in the values and focus on the signs.]

Based on my discussion to this point, I hope you can now see how the apparent (sign) discrepancies can be resolved when you consider what the poles of the factors actually reflect.

As I noted earlier, it is perfectly permissible to multiply the loadings on the factors containing an apparent reversal of poles by -1 and report on those loadings. Additionally, you can multiply the correlations in the factor correlation matrix between factors with reversed poles AND those without by -1 and report on these in a more intuitive fashion. However, you should NOT multiply the correlation involving factors involving reversed poles by -1. 

Here is the factor pattern matrix after multiplying the Factor 2 and 3 loadings by -1. 

For a closer look at the table, click here.

With respect to the factor correlations, we can multiply the correlations between Factor 1 and Factor 2 and between Factor 1 and Factor 3 by -1. These correlations are r=.16 and .10, respectively. We would not multiply the correlation between Factor 2 and 3 by -1. We leave it as r=.34.

***Important: Although I concentrated the bulk of this discussion on the factor pattern matrix, the same statements concerning the polarities of the factors apply with respect to the structure matrix.

*******************************************************

PAF with Varimax rotation

A different way of performing rotation is to force the factors to remain uncorrelated following rotation. This is referred to as orthogonal rotation. A very popular type of orthogonal rotation is Varimax rotation. To perform this analysis using EFA.dimensions requires a very simple change to the syntax we wrote earlier when we requested Promax rotation. In effect, we remove the ppower = 3 argument and modify the rotate argument so that it is rotate="VARIMAX" (see below).

All the pre-rotation results shown in the tables above will be exactly the same in the current analysis. As such, I do not reproduce them here. The only difference in output concerns the results following rotation of the factors. 

Below is the table of rotated loadings. Since the factors remain uncorrelated after rotation, this matrix can be considered a pattern matrix (under the assumption of factors correlated at 0) or a structure matrix. In effect, the loadings are zero-order correlations between each item and each factor. This is why there is only one loading matrix following rotation. 

The following part of the output contains the eigenvalues (Sum of Squared Loadings) and proportion of variance accounted for by each factor. The eigenvalues are computed as the sum of the squared loadings in the rotated factor matrix (above). The proportion of variance accounted for is computed by dividing each eigenvalue by the total number of variables (17). The proportion of variance accounted for by Factor 1 is 2.26/17 = .13 (or 13%). The proportion of variance accounted for by Factor 2 is 1.17/17 = .068 (or approximately 7%). The proportion of variance accounted for by Factor 3 is .93/17 = .054 (the roughly 6% you see in the table below). The total variance accounted for by the set of factors is .26 (or 26%). This is the same proportion of variance accounted for prior to rotation.  

Here are the loadings associated with the item content. We see the same items met the inclusion criterion on their factors following Varimax rotation as what we saw previous when Promax rotation was used. As before, we see the items meeting the loading criterion on factors 2 and 3 had negative loadings (changing the poles of these factors). 

For a closer look at the table, click here.

Here is the structure matrix after multiplying the loadings for factor 2 and factor 3 by -1. 

For a closer look at the table, click here.

 References

Cerny, B. A., & Kaiser, H. F. (1977). A study of a measure of sampling adequacy for factor-analytic correlation matrices. Multivariate Behavioral Research, 12(1), 43–47.

Dziuban, C. D., & Shirkey, E. C. (1974). When is a correlation matrix appropriate for factor analysis? Psychological Bulletin, 31, 358-361.

Fabrigar, L. R., & Wegener, D. T. (2012). Exploratory factor analysis. Oxford University Press.

Hahs-Vaughn, D. L. (2016). Applied multivariate statistical concepts. New York: Routledge.

Kaiser, H. F. (1960). The application of electronic computers to factor analysis. Educational and Psychological Measurement, 20, 141–151.

Leal-Soto, F., Ferrer-Urbina, R. (2017). Three-factor structure for Epistemic Belief Inventory: A cross-validation study. PLoS ONE, 12 (3): e0173295. doi:10.1371/journal.pone.0173295

Pituch, K.A., & Stevens, J.P. (2016). Applied multivariate statistics for the social sciences (6th ed.). New York: Routledge.

Schraw, G., Bendixen, L. D., & Dunkle, M. E. (2002). Development and validation of the Epistemic Belief Inventory (EBI). In B. K. Hofer & P. R. Pintrich (Eds.), Personal epistemology: The psychology of beliefs about knowledge and knowing (pp. 261–275). Lawrence Erlbaum Associates Publishers.

Watkins, M. W. (2018). Exploratory factor analysis: A guide to best practice. Journal of Black Psychology, 44, 219-246.

Watkins, M. W. (2021). A step-by-step guide to exploratory factor analysis with R and RStudio. New York: Routledge.